Tabela trygonometryczna to standardowa tabela, która pomaga nam znaleźć wartości stosunków trygonometrycznych dla standardowych kątów, takich jak 0°, 30°, 45°, 60° i 90°. To składa się ze wszystkich sześciu stosunków trygonometrycznych: sinus, cosinus, tangens, cosecans, secans i cotangens.
Przyjrzyjmy się szczegółowo tabeli trygonometrii.
Spis treści
- Tabela trygonometryczna
- Tabela funkcji trygonometrycznych
- Sztuczka do nauczenia się współczynników trygonometrycznych
- Jak zapamiętać tabelę trygonometryczną
- Jak utworzyć tabelę trygonometryczną
- Wzory trygonometryczne
- Tabela tożsamości trygonometrycznych
- Przykłady tabel trygonometrycznych
Tabela trygonometryczna
Tabela trygonometryczna to układ wartości wszystkich sześciu funkcji trygonometrycznych dla ich wspólnych kątów w formie tabelarycznej.
Notatka – Trygonometria to dział matematyki zajmujący się zależnościami pomiędzy kątami i bokami trójkątów prostokątnych.
Tabela funkcji trygonometrycznych
Trygonometria ma 6 podstawowych funkcji trygonometrycznych, którymi są sinus, cosinus, tangens, cosecans, secans i cotangens. Przyjrzyjmy się teraz funkcjom trygonometrycznym.
Dla dowolnego trójkąta prostokątnego z prostopadłą (P), podstawą (B) i przeciwprostokątną (H) sześć funkcji trygonometrycznych jest następujących:
| Tabela funkcji trygonometrycznych | |||
| Funkcjonować | Definicja | Reprezentacja | Związek z bokami trójkąta prostokątnego |
| Jego | Stosunek prostopadłej i przeciwprostokątnej | bez I | Strona przeciwna / Przeciwprostokątna |
| Cosinus | Stosunek podstawy i przeciwprostokątnej | sałata I | Sąsiednia strona / Przeciwprostokątna |
| Tangens | Stosunek sinusa i cosinusa kąta | Więc I | Strona przeciwna / Strona sąsiednia |
| Cosekans | Odwrotność grzechu θ | csc I lub cosek I | Przeciwprostokątna / Strona przeciwna |
| Sieczna | Odwrotność cos θ | sek I | Przeciwprostokątna / Sąsiednia strona |
| Cotangens | Odwrotność tan θ | łóżko składane I | Strona sąsiadująca / Strona przeciwna |
Notatka – Trygonometria to dziedzina matematyki zajmująca się związkami pomiędzy kątami i bokami trójkątów, zwłaszcza trójkątów prostokątnych. Polega na badaniu i zastosowaniu sinusów, cosinusów, tangensów i innych funkcji trygonometrycznych do rozwiązywania problemów z różnych dziedzin.
Sprawdzać : Trygonometria: wzory, tabela, tożsamości i stosunki
Sztuczka do nauczenia się współczynników trygonometrycznych
Przestudiuj tabelę omówioną poniżej, aby poznać stosunki trygonometryczne w łatwy do zapamiętania sposób.
| Niektórzy ludzie mają kręcone czarne włosy, aby wyglądać pięknie |
| sin θ (Niektórzy) = Prostopadła (ludzie) / przeciwprostokątna (mają) |
| cos θ (kręcone) = podstawa (czarna) / przeciwprostokątna (włosy) |
| tan θ (do) = prostopadły (produkt) / podstawa (piękno) |
Jak zapamiętać tabelę trygonometryczną
Tabela trygonometryczna jest dość łatwa do zapamiętania, jeśli znasz wszystkie wzory trygonometryczne. Istnieje również trik tzw sztuczka na jedną rękę zapamiętać tablicę trygonometryczną.

Krok 1: Na powyższym rysunku dla tabeli sinusów policz palce po lewej stronie dla standardowego kąta.
Krok 2: Podziel liczbę palców po lewej stronie (oblicz w pierwszym kroku) przez 4
Krok 3: Znajdź pierwiastek kwadratowy z wartości obliczonej w kroku 2.
Sprawdzać: Wzory trygonometryczne – lista wszystkich tożsamości i wzorów trygonometrycznych
Jak utworzyć tabelę trygonometryczną
Przeanalizuj poniższe kroki, aby utworzyć tabelę trygonometryczną dla kątów standardowych.
Krok 1: Utwórz tabelę
Utwórz tabelę i wypisz wszystkie kąty, takie jak 0°, 30°, 45°, 60° i 90°, w górnym rzędzie. Wpisz wszystkie funkcje trygonometryczne sin, cos, tan, cosec, sec i cot w pierwszej kolumnie.
Krok 2: Oblicz wartość wszystkich kątów funkcji sin.
Aby znaleźć wartości funkcji sin, podziel 0, 1, 2, 3 i 4 przez 4 i weź pod pierwiastek każdej wartości odpowiednio jako:
Bo wartość grzech 0° = √(0/4) = 0
Podobnie,
grzech 30° = √(1/4) = 1/2
grzech 45° = √(2/4) = 1/√2
grzech 60° = √(3/4) = √3/2
grzech 90° = √(4/4) = 1
| bez 0° | bez 30° | bez 45° | bez 60° | bez 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Krok 3: Oblicz wartość wszystkich kątów funkcji cos
Wartość funkcji cos jest przeciwieństwem wartości funkcji sin, tj. cos 0° = sin 90°, cos 30° = sin 60° i cos 45° = sin 45°, więc
| cos 0° | co 30° | co 45° | co 60° | co 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Krok 4: Oceń wartość wszystkich kątów funkcji tan
Wartość funkcji tan jest równa funkcji sin podzielonej przez funkcję cos, tj. tan x = sin x / cos x. Wartość wszystkich kątów w funkcji tan jest obliczana jako:
tan 0°= sin 0° / cos 0° = 0/1 = 0, podobnie
| więc 0° | więc 30° | więc 45° | więc 60° | więc 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Nie określono |
Krok 5: Oblicz wartości wszystkich kątów funkcji cosec
Wartość funkcji cosec jest równa odwrotności funkcji sin. Wartość cosec 0° otrzymuje się poprzez odwrotność sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = nieokreślony. Podobnie,
sts pobierz
| cosek 0° | cosek 30° | cosec 45° | cosek 60° | cosek 90° |
|---|---|---|---|---|
| Nie określono | 2 | √2 | 23 | 1 |
Krok 6: Oblicz wartość wszystkich kątów funkcji sec
Wartość funkcji sec jest równa odwrotności funkcji cos. Wartość sec 0° otrzymuje się poprzez odwrotność cos 0°
s 0° = 1 / cos 0° = 1 / 1 = 1. Podobnie
| sek. 0° | sek. 30° | sek. 45° | sek. 60° | sek. 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Nie określono |
Krok 7: Oceń wartość wszystkich kątów funkcji łóżeczkowej
Wartość funkcji cot jest równa odwrotności funkcji tan. Wartość cot 0° otrzymuje się poprzez odwrotność tan 0°
łóżko 0° = 1 /brązowe 0° = 1 / 0 = Nie określono. Podobnie,
| łóżeczko 0° | łóżeczko 30° | łóżeczko 45° | łóżeczko 60° | łóżeczko 90° |
|---|---|---|---|---|
| Nie określono | √3 | 1 | 1/√3 | 0 |
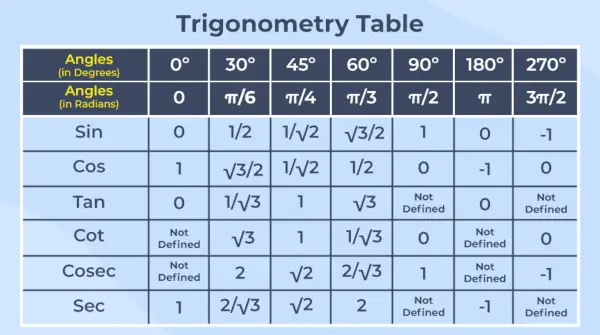
W ten sposób możemy stworzyć następującą tabelę stosunków trygonometrycznych:
| Stopnie i radiany Tabela trygonometryczna | |||||||
|---|---|---|---|---|---|---|---|
| Kąt (w stopniach) | Kąt (w radianach) | Bez | Sałata | Więc | Cosek | sek | Łóżko składane |
| 0° | 0 | 0 | 1 | 0 | Nieokreślony | 1 | Nieokreślony |
| 30° | str. 6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | s./4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | s./3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | str./2 | 1 | 0 | Nieokreślony | 1 | Nieokreślony | 0 |
Wzory trygonometryczne
Poznajmy niektóre wzory trygonometryczne związane z kątami dopełniającymi i uzupełniającymi.
- Kąty komplementarne: Para kątów, których suma wynosi 90°
- Kąty dodatkowe: Para kątów, których suma wynosi 180°
Sprawdzać: Stosunki trygonometryczne
Tożsamości trygonometryczne kątów dopełniających
Tożsamości kątów dopełniających opierają się na związku między funkcjami trygonometrycznymi dwóch kątów, które sumują się do 90 stopni (lub π/2 radianów). Są to tzw tożsamości współfunkcyjne .
| Funkcja trygonometryczna | Tożsamość |
|---|---|
| Jego | grzech(90°− I )=kos I |
| Cosinus | cos(90°− I )=bez I |
| Tangens | tan(90°− I ) = łóżeczko dziecięce I |
| Cotangens | łóżeczko dziecięce (90°− I )=tak I |
| Sieczna | s(90°− I )=csc I |
| Cosekans | cosec(90°− I )=sek I |
Tożsamości trygonometryczne kątów dodatkowych
Tożsamości kątów dodatkowych odnoszą się do funkcji trygonometrycznych dwóch kątów, które sumują się do 180 stopni (lub π radianów).
| Funkcja trygonometryczna | Tożsamość |
|---|---|
| Jego | grzech(180°− I )=bez I |
| Cosinus | cos(180°− I )=−cos I |
| Tangens | opalenizna (180°− I )=−brązowy I |
| Cotangens | łóżeczko dziecięce (180°− I )=−łóżeczko dziecięce I |
| Sieczna | s(180°− I )=−sek I |
| Cosekans | cosek(180°− I )=cosek I |
Tabela tożsamości trygonometrycznych
Tożsamości trygonometryczne są tożsamościami często używanymi w rozwiązywaniu problemów trygonometrycznych. Istnieją różne tożsamości trygonometryczne, ale trzy główne tożsamości trygonometryczne to:
| Tabela tożsamości trygonometrycznych | |
| Tożsamość trygonometryczna | Formuła |
| Tożsamość Pitagorasa | bez2θ + sałata2θ = 1 |
| Tożsamość sieczna-styczna | sek2θ – tak2θ = 1 |
| Tożsamość cosecans-cotangens | cosek2θ – łóżeczko2θ = 1 |
Sprawdź także:
- Stosunki trygonometryczne
- Odwrotne tożsamości trygonometryczne
- Wysokości i odległości
Przykłady tabel trygonometrycznych
Rozwiążmy kilka pytań na stole trygonometrycznym.
Przykład 1: Jeśli sin θ = 4/5, znajdź wszystkie wartości trygonometryczne.
Rozwiązanie:
Mamy tutaj,
grzech θ = 4/5
Algorytm „prima”as, sin θ = prostopadła / przeciwprostokątna
więc mamy prostopadłą (P) = 4 i przeciwprostokątną (H) = 5
Czyli zgodnie z twierdzeniem Pitagorasa H 2 = P 2 +B 2
Znajdźmy wartość podstawy (B)
52= B2+ 42
25 = B2+ 16
25 -16 = B2
B2= 9
B = 3Teraz mamy,
Sin θ = prostopadłość/przeciwprostokątna
= AB/AC = 4/5Cosinus θ = podstawa/przeciwprostokątna
= BC/AC = 3/5Styczna θ = prostopadła/podstawa
= AB/BC = 4/3Cosecans θ = przeciwprostokątna/prostokątna
= AC/AB = 5/4Sieczna θ = przeciwprostokątna/podstawa
= AC/BC = 5/3Cotangens θ = podstawa/prostopadła
= BC/AB = 3/4
Przykład 2: Znajdź wartość cos 45° + 2 sin 60° – tan 60°.
Rozwiązanie:
Z tabeli trygonometrii
cos 45° = 1/√2, sin 60° = √3/2 i tan 60° = √3
Zatem,
cos 45° + 2 grzech 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Przykład 3: Znajdź wartość cos 75°.
Rozwiązanie:
Wiemy to,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – grzech A grzech B}
= cos 45° cos 30° – grzech 45° grzech 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Wniosek – tabela trygonometryczna
Tabela trygonometrii zawiera obszerne odniesienia do funkcji trygonometrycznych sinus, cosinus, tangens, cosecans, secans i cotangens, wraz z ich odpowiednimi wartościami dla różnych kątów. I t służy jako cenne narzędzie do rozwiązywania problemów równania trygonometryczne, analiza zależności geometrycznych i zrozumienie zachowania zjawisk okresowych. Pogoda w matematyki, fizyki, inżynierii lub innych dziedzin, tabela trygonometryczna pomaga w obliczeniach, rozwiązywaniu problemów i wizualizacji, przyczyniając się do głębszego zrozumienia pojęć trygonometrycznych i ich zastosowań w scenariuszach ze świata rzeczywistego.
Tabela trygonometryczna – często zadawane pytania
Co to jest trygonometria?
Trygonometria to dział matematyki zajmujący się kątami i bokami dowolnego trójkąta.
Co to jest tabela trygonometryczna?
Tabela trygonometryczna to tabela zawierająca wartości wszystkich sześciu funkcji trygonometrycznych dla wspólnych kątów.
Kto wynalazł tablicę trygonometryczną?
Astronom grecki Hipparch (127 p.n.e.) wynalazł tablicę trygonometryczną.
Co to są kąty standardowe w tabeli trygonometrycznej?
Standardowe kąty w tabeli trygonometrycznej to 0°, 30°, 45°, 60° i 90°
Jaka jest wartość opalenizny 45 stopni?
Wartość tan 45 stopni wynosi 1.
Jak nauczyć się tabeli trygonometrii?
Sztuczka przy nauce tablicy trygonometrycznej polega na tym, że
- Musisz poznać wszystkie wartości wszystkich kątów funkcji grzechu.
- Wartość wszystkich kątów funkcji cos jest lustrzanym odbiciem funkcji sin.
- Wartości funkcji tan można obliczyć, dzieląc funkcję sin przez funkcję cos.
- Wartość funkcji cosec jest odwrotnością grzechu.
- Podobnie sec i cot są odwrotnością funkcji cos i cot.
Jakie są sześć podstawowych funkcji w tabeli trygonometrycznej?
Sześć podstawowych funkcji trygonometrycznych w tabeli trygonometrycznej to sinus, cosinus, tangens, secans, cotangens i cosecant.
Czy istnieją kalkulatory, które mogą zastąpić tabele trygonometrii?
Kalkulatory naukowe potrafią obliczyć stosunki trygonometryczne dla dowolnego kąta8.
Jakie jest zastosowanie tabeli trygonometrycznej?
Tabela trygonometryczna służy zasadniczo do znajdowania wartości wszystkich stosunków trygonometrycznych dla wszystkich kątów. Wartości te mają wiele zastosowań w życiu codziennym.
