Okrąg jednostkowy to okrąg, którego promień wynosi 1. Środek okręgu jednostkowego znajduje się w początku (0,0) osi. The obwód koła jednostkowego wynosi 2π jednostek, natomiast pole koła jednostkowego wynosi π jednostek2. Zawiera wszystkie właściwości Circle. Okrąg jednostkowy ma równanie x2+ i2= 1. To koło jednostkowe pomaga w definiowaniu różnych koncepcji trygonometrycznych.
Koło Jednostki
Koło Jednostki jest często oznaczane jako S1uogólnieniem na wyższe wymiary jest sfera jednostkowa. Przyjrzyjmy się bliżej bliżej okręgom jednostkowym, formule i rozwiązanym przykładom poniżej.
Co to jest okrąg jednostkowy?
Okrąg jednostkowy to okrąg o promieniu jednej (1) jednostki. Do narysowania okręgu jednostkowego używamy płaszczyzny kartezjańskiej, a okrąg jednostkowy jest dwustopniowym wielomianem z dwiema zmiennymi. Okrąg jednostkowy ma różne zastosowania w trygonometrii i algebrze i jest głównie używany do znajdowania wartości różnych stosunków trygonometrycznych, takich jak sin x, cos x, tan x i inne.
Definicja koła jednostkowego
W matematyce okrąg jednostkowy definiujemy jako miejsce stałego punktu znajdującego się w odległości jednej jednostki od środka okręgu. Okrąg jednostkowy ma promień jednej jednostki i stąd nazwa okrąg jednostkowy.
Równanie okręgu jednostkowego
Wiemy, że równanie dowolnego okręgu o środku (h, k) i promieniu „r” wygląda następująco:
(x – godz.) 2 + (y – k) 2 = r 2
W przypadku okręgu jednostkowego wiemy, że r wynosi 1 jednostkę, zatem równanie okręgu jednostkowego wygląda następująco:
(x – godz.) 2 + (y – k) 2 = 1
Formuła koła jednostkowego
Jeśli środkiem okręgu jednostkowego jest początek, tj. (h, k) = (0, 0), to równanie okręgu jednostkowego wygląda następująco:
X 2 + i 2 = 1
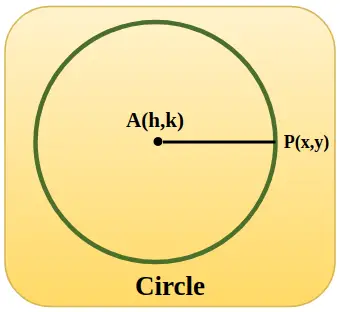
Okrąg jednostkowy jest przedstawiony na obrazku dodanym poniżej, ze współrzędnymi środka h, k, a gdy okrąg znajduje się w początku, wartość h i k wynosi zero, a promień AP jest równy 1 jednostce.
Funkcje trygonometryczne wykorzystujące okrąg jednostkowy
Do zrozumienia funkcji trygonometrycznych można lepiej zastosować twierdzenie Pitagorasa w okręgu jednostkowym. W tym celu rozważamy umieszczenie trójkąta prostokątnego wewnątrz okręgu jednostkowego w kartezjańskiej płaszczyźnie współrzędnych. Jeśli zauważymy, promień tego okręgu oznacza przeciwprostokątną trójkąta prostokątnego.
Promień okręgu tworzy wektor. Prowadzi to do powstania kąta, powiedzmy θ, z dodatnią osią x. Załóżmy, że x jest długością podstawy, a y wysokością trójkąta prostokątnego. Ponadto współrzędne punktów końcowych wektora promienia wynoszą odpowiednio (x, y).
Trójkąt prostokątny ma odpowiednio boki 1, x i y. Stosunek trygonometryczny można teraz obliczyć w następujący sposób:
sin θ = wysokość/przeciwprostokątna = y/1
cos θ = podstawa/przeciwprostokątna = x/1
Teraz,
- grzech θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Podstawiając wartości θ, możemy otrzymać główne wartości wszystkich funkcji trygonometrycznych. Podobnie spotykane są wartości funkcji trygonometrycznych przy różnych wartościach.
Okrąg jednostkowy z Sin Cos i Tan
Dowolny punkt na okręgu jednostkowym o współrzędnych (x, y) jest reprezentowany za pomocą tożsamości trygonometrycznych jako (cosθ, sinθ). Współrzędne rogów promienia reprezentują cosinus i sinus wartości θ dla określonej wartości θ i linii promienia. Mamy cos θ = x i sin θ = y. Istnieją cztery części koła, z których każda leży w jednej ćwiartce, tworząc kąty 90°, 180°, 270° i 360°. Wartości promieni mieszczą się odpowiednio w przedziale od -1 do 1. Ponadto wartości sin θ i cos θ mieszczą się odpowiednio w przedziale od 1 do -1.
Okrąg jednostkowy i tożsamości trygonometryczne
Tożsamości trygonometryczne okręgu jednostkowego dla cotangensu, siecznej i cosekanny można obliczyć przy użyciu tożsamości grzechu, cos i tan. Ostatecznie otrzymujemy trójkąt prostokątny o bokach odpowiednio 1, x i y. Obliczanie tożsamości okręgu jednostkowego można wyrazić jako:
- grzech θ = y/1
- cos θ = x/1
- tan θ = y/x
- s θ = 1/x
- cosec θ = 1/rok
- łóżko θ = x/y
Wykres koła jednostkowego
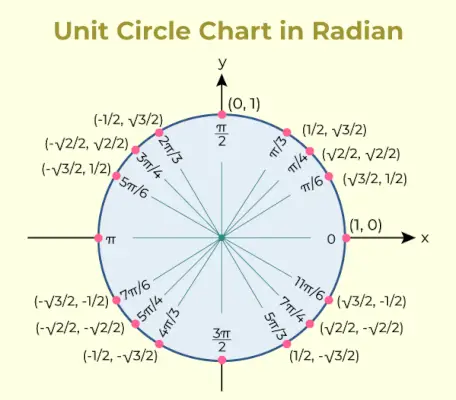
Wykres koła jednostkowego to wykres zawierający wartość funkcji trygonometrycznej sinus i cosinus dla różnych kątów. Wykres koła jednostkowego dla tego samego dodano poniżej,
wykonaj powłokę skryptu
Tabela okręgów jednostkowych
Stosunki trygonometryczne stosowane w tabeli okręgu jednostkowego służą do wyszczególnienia współrzędnych punktów na okręgu jednostkowym, które odpowiadają powszechnym kątom.
| Kąty | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| bez | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| sałata | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| Więc | 0 | 1/√(3) | 1 | √(3) | Nie określono |
| csc | Nie określono | 2 | √(2) | 23) | 1 |
| sek | 1 | 23) | √(2) | 2 | Nie określono |
| łóżko składane jak otworzyć ukryte aplikacje na Androidzie | Nie określono | √(3) | 1 | 1/√(3) | 0 |
Koło Jednostkowe Tożsamości Pitagorasa
Istnieją trzy tożsamości pitagorejskie i wszystkie z nich można łatwo udowodnić, korzystając z koncepcji okręgu jednostkowego, którymi są trzy tożsamości pitagorejskie:
- bez2θ + sałata2θ = 1
- 1 + tak2θ = sek2I
- 1 + łóżeczko dziecięce2θ = cosek2I
Płaszczyzna zespolona koła jednostkowego
Liczby zespolone i płaszczyznę zespoloną można łatwo wyjaśnić za pomocą koncepcji okręgu jednostkowego. Równanie okręgu jednostkowego w postaci zespolonej to:
|z| = 1
LUB
X 2 + i 2 = 1
W formie Eulera liczba zespolona jest reprezentowana jako:
z = mi To = sałata t + i(sin t)
Czytaj więcej
Rozwiązane przykłady na okręgu jednostkowym
Zadanie 1: Udowodnić, że punkt Q leży na okręgu jednostkowym, Q = [1/√(6), √4/√6]
Rozwiązanie:
Dany,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Równanie koła jednostkowego to:
X2+ i2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
Lewa strona ≠ prawa strona
Zatem punkt Q[1/√(6), √4/√6] nie leży na okręgu jednostkowym.
Pytanie 2: Oblicz więc 30 O używając wartości sin i cos koła jednostkowego.
Rozwiązanie:
javatpunkt java
tan 30° przy użyciu wartości sin i cos,
tan 30° = (sin 30°)/ (cos 30°)
- bez 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
Pytanie 3: Sprawdź, czy punkt P [1/2, √(3)/2] leży na okręgu jednostkowym.
Rozwiązanie:
Dany,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Równanie koła jednostkowego to:
- X2+ i2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Ćwicz pytania dotyczące okręgu jednostkowego
Pytanie 1. Sprawdź, czy punkty A (1/2, 3/2) leżą na okręgu jednostkowym.
Pytanie 2. Sprawdź, czy punkty A (2, 1/2) leżą na okręgu jednostkowym.
Pytanie 3. Znajdź wartość cos 240°
Pytanie 4. Znajdź wartość tan 320°
Pytanie 5. Znajdź wartość grzechu 160°
Koło Jednostki – Często zadawane pytania
Co to jest okrąg jednostkowy?
Okrąg jednostkowy definiuje się jako położenie punktu oddalonego o jedną jednostkę od stałego punktu. Ma środek w (0,0), a wartość jego promienia wynosi 1.
Jak sprawdzić, czy punkt leży na okręgu jednostki?
Dowolny punkt leżący na płaszczyźnie 2D mający postać (x, y) jest umieszczany w równaniu okręgu jednostkowego x2+ i2= 1, aby sprawdzić, czy leży na okręgu, czy nie.
Jaki jest wzór na okrąg jednostkowy?
Wzór na okrąg jednostkowy to wzór używany do algebraicznego przedstawienia okręgu jednostkowego. Wzór na okrąg jednostkowy jest podany jako:
X 2 + i 2 = 1
Dlaczego nazywa się to kołem jednostkowym?
Okrąg jednostkowy nazywany jest okręgiem jednostkowym, ponieważ ma promień jednej (1) jednostki.
