the Funkcja cosinus albo sałata Krótko mówiąc, funkcja jest jedną z sześciu Funkcje trygonometryczne podstawy trygonometrii. Cosinus w trygonometrii podawany jest jako stosunek podstawy do przeciwprostokątnej trójkąta prostokątnego. Funkcja cosinus jest reprezentowana jako Cos x, gdzie x to kąt, dla którego obliczany jest współczynnik cosinus. Jeśli chodzi o funkcję, możemy powiedzieć, że x jest wejściem lub dziedziną funkcji cosinus.

Jest szeroko stosowany w szerokim zakresie przedmiotów, takich jak fizyka, geometria i inżynieria, między innymi ogólnie poprzez wykorzystanie jego okresowego charakteru. Na przykład służy do definiowania falowej natury fal dźwiękowych, obliczania strumienia elektrycznego przez płaską powierzchnię itp. W tym artykule dowiadujemy się szczegółowo, czym jest funkcja cosinus, domena i zakres funkcji cosinus, okres i wykres funkcji cosinus.

Spis treści

• Co to jest funkcja cosinus?
• Cos w okręgu jednostkowym
• Wykres funkcji cosinus
• Odwrotność funkcji cosinus
• Funkcja cosinus w rachunku różniczkowym
• Tożsamości funkcji Cos

Co to jest funkcja cosinus?

Funkcja cosinus jest funkcją trygonometryczną, która ma zasadniczo charakter okresowy. Funkcja cosinus jest wyrażana jako cos x, gdzie x jest jednym z kątów ostrych trójkąta prostokątnego. Funkcja cosinus znajduje stosunek podstawy i przeciwprostokątnej dla danej wartości x. Funkcja cosinus jest skracana jako cos(x) lub cos(θ), gdzie x to kąt w radianach, a theta θ to kąt w stopni ogólnie. Funkcję cosinus można zdefiniować za pomocą okręgu jednostkowego, tj. okręgu o promieniu jednostkowym, jak zobaczymy w dalszej części tego artykułu. Ma charakter okresowy i powtarza swoje wartości po każdym pełnym obrocie kątów. Na płaszczyźnie kartezjańskiej można ją nazwać składową wektorową przeciwprostokątnej równoległą do osi x.

Definicja funkcji cosinus

Funkcję cosinus definiuje się w trójkącie prostokątnym jako stosunek długości boku sąsiadującego z danym kątem do długości przeciwprostokątnej. Matematycznie funkcja cosinus jest podana jako

Cos x = Cos θ = długość podstawy/długość przeciwprostokątnej = b/h = OB/OA

Gdzie X to kąt w radianach, a θ to równoważny kąt w stopniach.

Dziedzina i zakres funkcji Cos

Wiemy, że w przypadku funkcji dziedzina to dopuszczalne wartości wejściowe, a zakres to wartość wyjściowa dla tej konkretnej wartości wejściowej lub dziedziny. Można zatem założyć, że funkcja działa jak procesor, który pobiera dane wejściowe, przetwarza je i daje określony wynik. Dziedzinę i zakres funkcji cos omówiono poniżej:

• Dziedzina funkcji cosinus: R tj. zbiór wszystkich liczb rzeczywistych.
• Zakres funkcji cosinus: [-1, 1], tj. wynik różni się pomiędzy wszystkimi liczbami rzeczywistymi od -1 do 1.

Okres funkcji cosinus

The funkcjonować ma charakter okresowy, tj. powtarza się po 2π lub 360°. Innymi słowy, powtarza się po każdym pełnym obrocie. Stąd okres funkcji cosinus to pełny obrót lub kąt 360° (lub 2π).

Odwrotność funkcji cosinus

Odwrotność funkcji cosinus jest znana jako sieczna funkcja lub sek w skrócie. Matematycznie odwrotność funkcji cosinus jest podana jako

3d w autocadzie

s(θ) = 1/cos(θ)

Zgodnie z regulaminem Wzajemność , jeśli pomnożymy Cos x przez Sec x, iloczyn zawsze będzie wynosić 1.

Wykres funkcji cosinus

Wykres funkcji cosinus przypomina wykres funkcji sinus z tą podstawową różnicą, że dla x = 0 wykres funkcji sin przechodzi od początku, natomiast przy x = 0 wykres funkcji cosinus przechodzi od (0, 1) w y-aix. Poniżej znajduje się wykres wartości funkcji cosinus, tj. y = cos x

Właściwości omówione powyżej można zobaczyć na wykresie, podobnie jak okresowy charakter funkcji.

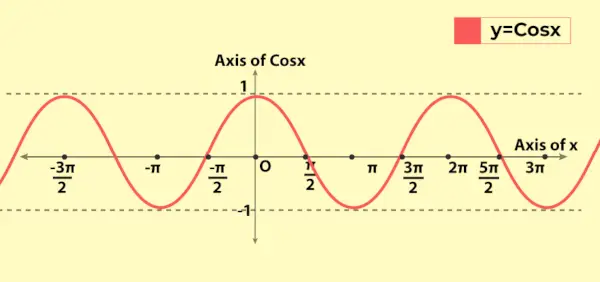
Zmiana funkcji cosinus na wykresie

Ponieważ zakres funkcji cosinus wynosi [-1, 1], dlatego na wykresie waha się od -1 do 1. Wykazuje swój okresowy charakter, gdyż wykres powtarza się po każdej długości 2π na osi x. Odzwierciedla to fakt, że funkcja cosinus ma okres 2π (lub 360°).

Cos w okręgu jednostkowym

Cosinus Funkcję można zdefiniować za pomocą okręgu jednostkowego. Rozumiemy, jak możemy zdefiniować funkcję cosinus za pomocą koła jednostkowego.

Rozważmy odcinek OA obracający się wokół punktu O, gdzie O jest początkiem płaszczyzny kartezjańskiej. Zatem obrót OA opisuje okrąg jednostkowy (okrąg o promieniu jednostkowym) ze środkiem w początku O, a punkt A zawsze leży na tym okręgu. Jeśli upuścimy prostopadłą z A na oś x i nazwiemy punkt przecięcia B, a θ jest kątem, jaki OA tworzy z dodatnim kierunkiem osi x, to cos(θ) = rzut przeciwprostokątnej na x -oś = OB/|OA| = OB (ponieważ |OA| = 1 jednostka).

Należy pamiętać, że kierunek OB jest ważny, co widać na poniższych rysunkach. Zielony segment oznacza długość/wielkość, a strzałka oznacza kierunek (+ve lub -ve) cos(θ)

Należy zauważyć, że wartość cos(θ) jest dodatnia dla θ należącego do pierwszej i czwartej ćwiartki, natomiast ujemna dla θ należącego do drugiej i trzeciej ćwiartki.

Odwrotność funkcji cosinus

Odwrotność funkcji cosinus znanej jako arc-cosinus funkcja i w skrócie jako arccos(x) Lub sałata ^-1 (X) definiuje się następująco

cos(x) = y

⇒ kosm ^-1 (y) = x

Dziedzina i zakres funkcji odwrotnej cosinus

Dziedzina i zakres funkcji odwrotnej cosinus są wymienione poniżej:

• Dziedzina funkcji odwrotnej cosinus: Wszystkie liczby rzeczywiste w zakresie [-1, 1]
• Zakres funkcji odwrotnego cosinusa: Wszystkie liczby rzeczywiste w zakresie [0, π]

Funkcja cosinusa hiperbolicznego

Funkcje hiperboliczne są analogowym odpowiednikiem funkcji trygonometrycznej, której wyrażenie algebraiczne jest wyrażone w postaci funkcji wykładniczej. Funkcja cosinusa hiperbolicznego w skrócie cosh(x) Gdzie X jest kątem hiperbolicznym jest pojęciem geometrii hiperbolicznej. Like (cos(x), sin(x)) reprezentuje punkt na okręgu jednostkowym, (cosh(x), sinh(x)) reprezentuje punkt na hiperboli jednostkowej, tj. xy = 1, gdzie sinh(x) oznacza hiperbolę funkcja sinus. Algebraiczne rozwinięcie hiperbolicznej funkcji cos jest podane jako

cosh(x) = (np ^X + i ^-X )/2

Więcej szczegółów na temat funkcji hiperbolicznych wykracza poza zakres tego artykułu, ale możesz się do nich odwołać Ten artykuł .

Funkcja cosinus w rachunku różniczkowym

Dział rachunku matematycznego zajmuje się różnicowanie i integracja danej funkcji. Różniczkowanie funkcji to szybkość zmian funkcji względem zmiennej niezależnej, natomiast całkowanie to proces odwrotny do różniczkowania, który polega na znalezieniu całki z funkcji, której pochodna istnieje.

Pochodna funkcji cosinus

The pochodna funkcji cosinus jest równa wartości ujemnej funkcji sinus. Matematycznie

d(cos(x))/dx = -sin(x)

Całkowanie funkcji cosinus

The Całka nieoznaczona funkcji cosinus jest równy funkcji sinus. Matematycznie -

∫cos(x)dx = sin(x) + C, gdzie C jest stałą całkowania.

Funkcje sinus i cosinus

Poniższy wykres przedstawia kluczową różnicę między funkcją sinus i cosinus:

Różnica między funkcjami sinus i cosinus

Poniższa tabela przedstawia różnice między funkcją sinus i cosinus –

Tabela wartości cos

Poniższa tabela przedstawia wartości funkcji cosinus dla niektórych typowych kątów w pierwszej ćwiartce płaszczyzny kartezjańskiej –

Możemy łatwo obliczyć wartości innych typowych kątów, takich jak 15°, 75°, 195°, -15° itd., korzystając z tych wartości, używając wzorów cos (x + y) i cos (x – y) opisanych w dalszej części tego artykuł.

Sprawdzać, Tabela trygonometryczna

Tożsamości funkcji Cos

Poniżej wymieniono podstawowe tożsamości trygonometryczne związane z funkcją cosinus:

• bez²(x) + sałata²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + grzech(x)grzech(y)
• cos(-x) = cos(x)
• cos(x) = 1/s(x)
• cos 2x = sałata²x – grzech²x = 1 – 2 grzech²x = 2cos²x – 1 = (1 – tan²x/1 + opalenizna²X)
• sałata 3x = 4cos³x – 3cos x

Powiązane artykuły

• Różniczkowanie funkcji trygonometrycznych
• Odwrotne funkcje trygonometryczne
• Odwrotne pochodne trygonometryczne

Rozwiązane przykłady funkcji cosinus

Oto kilka rozwiązanych przykładów, które pomogą Ci lepiej zrozumieć koncepcję funkcji cosinus.

Przykład 1: Jakie są maksymalne i minimalne wartości funkcji cosinus?

Rozwiązanie:

Maksymalna wartość funkcji cosinus wynosi 1 przy 0° i 180°, natomiast minimalna wartość funkcji wynosi -1 przy 180°.

Przykład 2: Pod jakim kątem w zakresie [0, 360] wartość funkcji cosinus wynosi 0?

Rozwiązanie:

Wartość funkcji cosinus wynosi 0 przy kątach 90° i 270°.

Przykład 3: Dla jakich ćwiartek wartość funkcji cosinus jest ujemna?

Rozwiązanie:

Funkcja cosinus jest ujemna w II^IIi III^{r & D}ćwiartki.

Przykład 4: Oblicz wartość cos (45°).

Rozwiązanie:

węzeł listy Java

Zgodnie z tożsamością 4 podaną powyżej, cos(-x) = cos(x).

Zatem cos(-45°) = cos(45°) = 1/√2

Przykład 5: Oblicz wartość cos(15°).

Rozwiązanie:

Używając tożsamości 3 podanej powyżej –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Przykład 6: Co to jest cos ^-1 (1/2) w zakresie [0,π]?

Rozwiązanie:

Niech cos^-1(1/2) = y.

Zatem cos(y) = 1/2 ⇒ y = π/3 w podanym powyżej zakresie.

Stąd odpowiedź brzmi π/3.

Przykład 7: Jaka jest wartość cos(-15°)?

Rozwiązanie:

Używając tożsamości 3 podanej powyżej –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternatywnie możemy również użyć tożsamości cos(-x) = cos(x) i użyć wartości cos(15°) obliczonej w przykładzie 5.

Przykład 8: Oblicz pole pod wykresem funkcji cosinus dla x = 0 do x = π/2.

Rozwiązanie:

Podaną powierzchnię można obliczyć rozwiązując całkę oznaczoną –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Zatem odpowiedź brzmi: 1 jednostka kwadratowa.

Przykład 9: Jeśli cos(x) = π/3, znajdź wartość cos(3x) (w postaci dziesiętnej z dokładnością do dwóch miejsc po przecinku).

Rozwiązanie:

Korzystając z tożsamości – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Przykład 10: Znajdź wartość cos(120°).

Rozwiązanie:

Używanie tożsamości dla cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 grzech²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Ćwicz pytania: Funkcje Cos

Pytanie 1. Jaki jest wzór na obliczenie cos kąta w trójkącie prostokątnym?

Pytanie 2. Jaka jest interpretacja geometryczna cos na płaszczyźnie kartezjańskiej?

Pytanie 3. Oblicz wartość cos(120°).

Pytanie 4. Znajdź wartość cos ^-1 (√3/2) w zakresie [π, 2π].

Pytanie 5. Jeśli słup rzuca na ziemię cień tej samej długości, znajdź kąt słońca względem ziemi, jeśli słońce jest skierowane na wschód.

Podsumowanie – Funkcja cosinus

Funkcja cosinus, oznaczona jako cos(x), jest podstawową funkcją trygonometryczną zdefiniowaną jako stosunek podstawy do przeciwprostokątnej w trójkącie prostokątnym i jest niezbędna w różnych dziedzinach, takich jak fizyka, inżynieria i geometria, ze względu na jej okresowy charakter , co odgrywa zasadniczą rolę w modelowaniu zachowań fal. Ma dziedzinę wszystkich liczb rzeczywistych i zakres od -1 do 1, powtarzając swój cykl co 2 Liczba Pi radianów lub 360 stopni, co widać na wykresie przypominającym falę, który zaczyna się od (0,1). W rachunku różniczkowym pochodna cos(x) to − sin( X ), a jej całka daje grzech ( X )+ C , gdzie C jest stałą całkowania. Funkcja ta rozciąga się również na formy hiperboliczne, takie jak cosh(x), zwiększając jej zastosowanie w różnych kontekstach i rozwiązaniach matematycznych, w tym w obliczeniach fal i oscylacjach w układach fizycznych.

Funkcja cosinus: często zadawane pytania

1. Co to jest funkcja cosinus?

Funkcja cosinus jest jedną z podstawowych funkcji trygonometrycznych. Definiuje się go w trójkącie prostokątnym jako stosunek długości boku sąsiadującego z danym kątem do długości przeciwprostokątnej.

2. Czy cos i cosinus są takie same w trygonometrii?

Tak. cos jest skrótem/skróconą formą funkcji cosinus.

3. Jaki jest zakres funkcji Cos?

Zakres funkcji cos lub cosinus to wszystkie liczby rzeczywiste z zakresu od -1 do 1, tj. [-1,1].

4. Jaka jest dziedzina funkcji Cos?

Dziedziną funkcji cos lub cosinus jest ser wszystkich liczb rzeczywistych, tj. R .

5. Jaka jest maksymalna wartość funkcji cosinus?

Maksymalna wartość funkcji cosinus wynosi 1 dla wszystkich kątów odpowiadających 0° lub 360°.

6. Jaka jest minimalna wartość funkcji cosinus?

Minimalna wartość funkcji cosinus wynosi -1 dla wszystkich kątów odpowiadających 180°.

7. Jak znaleźć wartość Cos(-x)?

Wartość cos(-x) można obliczyć obliczając wartość cos(x) ze względu na istnienie tożsamości: cos(-x) = cos(x).

8. Jak wykreślić funkcję cosinus?

Aby narysować wykres funkcji cosinus na płaszczyźnie kartezjańskiej, odnieś się do osi x przedstawiającej kąty w radianach (lub stopniach), a osi y do przedstawiania wartości funkcji cosinus dla odpowiedniego kąta na osi x. Teraz,

• Krok 1: Weź podzbiór osi x, dla którego chcesz narysować wykres.
• Krok 2: Podziel oś x w tym zakresie na równoodległe punkty (tj. pomiędzy wszystkimi podpunktami jest równa przestrzeń). Należy pamiętać, że im większa liczba podziałów, tym większa precyzja powstałego wykresu.
• Krok 3: Dla każdego z tych podpunktów x zaznacz na wykresie punkt (x, cos(x)).
• Krok 4: Połącz wszystkie zaznaczone punkty, aby otrzymać wykres funkcji cosinus (dla wybranego podzbioru osi x).

9. Jak znaleźć okres funkcji cosinus?

Okres funkcji cosinus oznacza minimalny zakres wartości, po którym funkcja zaczyna się powtarzać. Wiemy, że funkcja cosinus powtarza się po każdym pełnym obrocie, co oznacza 2π radianów. Dlatego okres funkcji cosinus wynosi 2π radianów, czyli 360°.

10. Co to jest amplituda funkcji cosinus?

Amplituda funkcji cosinus odnosi się do maksymalnego przesunięcia wartości funkcji od położenia średniego, tj. osi x. Amplituda funkcji cosinus wynosi 1, ponieważ maksymalne przemieszczenie wynosi 1 (dla wartości -1 i 1 odpowiednio przy 180 i 0 stopniach. Należy zauważyć, że zakres funkcji cosinus wynosi [-amplituda, amplituda).