A Funkcjonować w matematyce jest to szczególna relacja pomiędzy zbiorem wartości wejściowych i zbiorem wartości wyjściowych. W funkcji każda wartość wejściowa daje określoną wartość wyjściową. Reprezentujemy funkcję w matematyce jako, y = f(x) gdzie X jest wartością wejściową i dla każdego X otrzymujemy wartość wyjściową jako y.

W tym artykule dowiemy się m.in. funkcje w matematyce, ich rodzaje, przykłady i inne szczegóły.

Spis treści

• Co to jest funkcja w matematyce?
• Definicja funkcji w matematyce
• Funkcje Przykłady
• Warunek funkcji
• Reprezentacja funkcji w matematyce
• Identyfikacja funkcji
• Rodzaje funkcji
• Co to jest funkcja w algebrze?
• Dziedzina i zakres funkcji
• Skład funkcji
• Algebra funkcji
• Co to jest funkcja na wykresie?
• Funkcje graficzne
• Wspólne funkcje
• Zastosowania funkcji
• Przykłady dotyczące funkcji
• Ćwicz problemy dotyczące tego, czym jest funkcja

Co to jest funkcja w matematyce?

Funkcja w matematyce to a relacja pomiędzy wartościami wejściowymi (dziedzina) i wartościami wyjściowymi (zakres) danych zbiorów w taki sposób, że żadne dwie zmienne ze zbiorów dziedzin nie są powiązane z tą samą zmienną w zestawie zakresów. Prostym przykładem funkcji matematycznej jest f(x) = 2x, która jest zdefiniowana na R → R. Tutaj każda zmienna w dziedzinie jest powiązana tylko z jedną zmienną w zakresie.

Funkcja w matematyce ma dziedzinę, kodomenę i zakres. Dziedzina to zbiór wszystkich możliwych wartości x, a zakres funkcji to zbiór wszystkich wartości wyjściowych y. Zakres jest podzbiorem kodomeny funkcji. Można również powiedzieć, że funkcja w matematyce jest relacją o unikalnym wyniku i żadne dwie wartości wejściowe nie mają podobnych wyników w funkcji, jak ma to miejsce w przypadku relacji.

Definicja funkcji w matematyce

Funkcja to specjalna relacja lub metoda łącząca każdy element zbioru A z unikalnym elementem zbioru B poprzez zdefiniowaną relację. Zbiór A nazywany jest dziedziną, a zbiór B współdziedziną funkcji. Funkcję matematyczną ze zbioru A do zbioru B definiuje się jako:

f = ∀ za ∈ ZA, b ∈ B

Każda funkcja jest relacją, ale nie każda relacja jest funkcją. Kryteria uznania relacji za funkcję, ponieważ w funkcji każdy element zbioru A ma tylko jeden obraz w zbiorze B, podczas gdy w relacji element zbioru A może mieć więcej niż jeden obraz w zbiorze B.

Definiujemy funkcje matematyczne od niepustego zbioru A do niepustego zbioru B w taki sposób, że:

(a, b) ∈ f, wtedy f(a) = b

gdzie dzwoniliśmy B jako obraz A zdefiniowane w relacji F .

Każdy element 'A' zestawu A ma unikalny obraz „ B ‘ w zbiorze B jest to funkcja.

Funkcje Przykłady

Funkcję w matematyce f definiuje się jako, y = f(x) gdzie X jest wartością wejściową i dla każdej wartości wejściowej x otrzymujemy unikalną wartość y. Różne przykłady funkcji matematycznych zdefiniowanych na R → R to:

• y = f(x) = 3x + 4
• y = f(x) = grzech x + 3
• y = f(x) = -3x²+ 3 itd

Warunek funkcji

Dla dowolnych dwóch niepustych zbiorów A i B funkcja f: A → B oznacza to F jest funkcją od A do B, gdzie A jest domeną i B jest współdomeną.

Dla dowolnego elementu a ∈ A, element unikalny, b ∈ B istnieje taki, że (a,b) ∈ f. Unikalny element b, który jest powiązany z a, jest oznaczony przez f(a) i odczytywany jako f z a. Można to lepiej zrozumieć na podstawie poniższego obrazka:

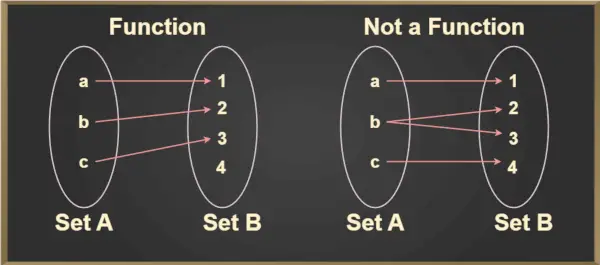
Test linii pionowej

Test linii pionowej służy do określenia, czy krzywa jest funkcją, czy nie. Jeśli jakakolwiek krzywa przecina linię pionową w więcej niż jednym punkcie, to krzywa nie jest funkcją.

Reprezentacja funkcji w matematyce

Reprezentujemy funkcję w matematyce jako,

y = f(x) = x + 3

Tutaj zbiór wartości x jest dziedziną funkcji, a zbiór wartości wyjściowych y jest współdziedziną funkcji. Tutaj funkcja jest zdefiniowana dla wszystkich liczb rzeczywistych, ponieważ daje unikalną wartość dla każdego x, ale nie zawsze jest możliwe uzyskanie wyniku dla każdej wartości x, w takim przypadku definiujemy funkcję w dwóch częściach, można to rozumieć jako

• f(x) = 1/(x – 2), gdzie x ≠ 2
• f(x) = x²gdzie x ∈ {R}

Funkcję w matematyce możemy zdefiniować jako maszynę, która pobiera pewne dane wejściowe i daje unikalny wynik. Funkcja f(x) = x²jest zdefiniowany poniżej jako,

Możemy przedstawić funkcję matematyczną trzema metodami jako:

• Zestaw uporządkowanych par
• Formularz tabeli
• Forma graficzna

Na przykład, jeśli reprezentujemy funkcję jako, f(x) = x³

Innym sposobem przedstawienia tej samej funkcji jest: zbiór uporządkowanych par Jak,

fa = {(1,1), (2,8), (3,27)}

W powyższym zbiorze dziedzina funkcji to D = {1, 2, 3}, a zakres funkcji to R = {1, 8, 27}

Identyfikacja funkcji

Funkcja jest klasyfikowana jako szczególny rodzaj relacji w matematyce. Do identyfikacji funkcji można zastosować następujące reguły:

• Relacja, w której każde wejście odwzorowane na unikalne wyjście jest funkcją. To wywołało funkcję jeden do jednego.
• Relacja, w której dwa wejścia (obraz wstępny) odwzorowane na jedno wyjście jest również funkcją. Jest to funkcja wiele do jednego.
• Relacja, w której jedno wejście jest odwzorowywane na dwa różne wyjścia, nie jest funkcją.
• Relacja, w której wiele danych wejściowych jest odwzorowanych na wiele wyjść zgodnie z żadną określoną regułą, nie jest funkcją.

Rodzaje funkcji

Różny Rodzaje funkcji służą do rozwiązywania różnego rodzaju problemów matematycznych, szczególnie związanych z krzywymi i równaniami. W matematyce istnieją trzy główne typy funkcji, które opierają się na mapowaniu elementów ze zbioru A do zbioru B.

Funkcja iniekcyjna lub funkcja jeden do jednego

Funkcja, w której każdy element domeny ma odrębny obraz w kodomenie, nazywana jest funkcją zastrzykowy Lub Funkcja jeden do jednego .

f: Mówi się, że A → B jest jeden do jednego lub iniekcyjne, jeśli obrazy różnych elementów A pod f są różne, tj.

fa ₁ ) = b ₁ , f(a ₂ ) = b ₂

gdzie₁, A₂∈ A i b₁, B₂∈ B

Funkcje surjektywne lub funkcja Onto

Funkcja surjektywna to funkcja, w której każdy element kodomeny ma obraz wstępny w domenie. Nazywa się to również Na funkcję co oznacza, że ​​każdy element kodomeny jest powiązany z każdym elementem domeny. Żaden element kodomeny nie powinien mieć pustej relacji. Liczba elementów kodomeny i zakresu jest taka sama.

f: Mówi się, że A → B jest na, jeśli każdy element B jest obrazem jakiegoś elementu A pod f, tj. dla każdego b ϵ B istnieje element „a” w A taki, że f(a) = b.

Funkcja bijektywna

Jeśli funkcja ma właściwości zarówno Injective (jeden do jednego), jak i Surjective (funkcja Onto), wówczas nazywa się ją a Funkcja bijektywna . W funkcji bijektywnej każdy element domeny jest powiązany z każdym elementem kodomeny, a także istnieje relacja jeden do jednego. Oznacza to, że liczba elementów kodomeny i zakresu jest taka sama i żaden element ani w domenie, ani w kodomenie nie ma pustej relacji.

Na podstawie wartości wyjściowych funkcje sklasyfikowano jako nieparzyste i parzyste. Przyjrzyjmy się im

Dziwne funkcje

Funkcja nieparzysta to rodzaj funkcji, która wykazuje symetrię względem początku. W szczególności, jeśli f(x) jest funkcją nieparzystą, pokazuje, że f(-x) = -f(x)

Nawet funkcja

Funkcja parzysta to rodzaj funkcji, która wykazuje symetrię względem osi y. W szczególności, jeśli f(x) jest funkcją parzystą, pokazuje, że f(-x) = f(x)

Co to jest funkcja w algebrze?

Funkcja w algebra to równanie, w którym dowolne x, które można umieścić w równaniu, da dokładnie jeden wynik, taki jak y z równania. Jest reprezentowany jako y = f(x), gdzie x jest zmienną niezależną, a y jest zmienną zależną.

Na przykład:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Dziedzina i zakres funkcji

Domena i zakres funkcji są odpowiednio wartością wejściową i wyjściową funkcji. Załóżmy na przykład, że mamy funkcję podaną jako f(x) = x². Tutaj możemy przyjąć całą liczbę rzeczywistą jako wartość wejściową x, a wynikiem będzie zawsze dodatnia liczba rzeczywista. Stąd jego dziedzina jest zbiorem wszystkich liczb rzeczywistych reprezentowanych jako R, podczas gdy jego zakres jest zbiorem dodatnich liczb rzeczywistych reprezentowanych jako R⁺

Skład funkcji

Jeżeli f: A → B i g: B → C będą dwiema funkcjami. Następnie złożenie f i g oznaczamy jako f(g) i definiujemy jako funkcję mgła = f(g(x)) dla x ∈ A.

Weźmy dwie funkcje f(x) = x + 3 i g(x) = 2x²

mgła = f(g(x))

⇒ mgła = f(2x²)

⇒ ząb = 2x²+ 3

Ucz się więcej, Skład funkcji

Algebra funkcji

Algebra funkcji obejmuje operacje algebraiczne wykonywane pomiędzy dwiema funkcjami. Poniżej wymieniono działania algebraiczne dla dwóch funkcji f(x) i g(x) zdefiniowanych na rzeczywistej wartości x:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Ponieważ k jest liczbą rzeczywistą}
• (f/g)(x) = f(x) /g(x); {Dla g(x) ≠ 0}

Co to jest funkcja na wykresie?

Funkcję można łatwo przedstawić na wykresie. Dowolna funkcja na wykresie reprezentuje krzywą (w tym linię prostą) w płaszczyźnie x-y odwzorowaną dla jej wartości wejściowych i odpowiadających im wartości wyjściowych.

Aby wykreślić funkcję, najpierw znajdź kilka punktów leżących na tej funkcji, a następnie połącz te punkty zgodnie z miejscem funkcji. Przykładowo do wykreślenia funkcji (prostej) f(x) = y = 5x – 2 potrzebny jest jakiś punkt na wykresie. Aby znaleźć punkt na wykresie, najpierw bierzemy losowe wartości x, a następnie znajdujemy odpowiadające im wartości y, jako:

f(x) = y = 5x- 2

jeśli x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

jeśli x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

jeśli x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Łącząc teraz te punkty otrzymamy wykres funkcji y = 5x – 2

Funkcje graficzne

Znajomość wartości x pozwala na przedstawienie funkcji f(x) na wykresie. Ponieważ y = f(x), możemy znaleźć powiązaną wartość y, zaczynając od wartości x. W rezultacie możemy wykreślić wykres w płaszczyźnie współrzędnych, używając wartości x i y. Rozważ następujący scenariusz:

Załóżmy, że y = x + 3

Gdy x = 0, y = 3

Podobnie,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

W rezultacie możemy wykreślić wykres funkcji x + 3, korzystając z tych wartości.

Wspólne funkcje

Poniżej omówiono niektóre wspólne funkcje powszechnie stosowane w matematyce:

Prawdziwa funkcja

Prawdziwa funkcja w matematyce odnosi się do funkcji, której dziedzina i zakres są podzbiorami liczb rzeczywistych (oznaczonych jako ℝ). Mówiąc prościej, funkcja rzeczywista to reguła matematyczna lub zależność, która przypisuje wartość liczby rzeczywistej do każdej wprowadzonej liczby rzeczywistej.

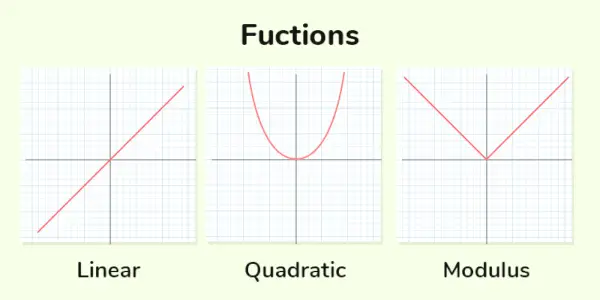
Prawdziwe funkcje

Funkcja wielomianu

Funkcja, w której wykładniki zmiennych algebraicznych są nieujemnymi liczbami całkowitymi, nazywa się Funkcja wielomianu . Jeśli potęga zmiennej wynosi 1, nazywa się ją funkcją liniową, jeśli potęga wynosi 2, nazywa się ją funkcją kwadratową, a jeśli potęga wynosi 3, nazywa się ją funkcją sześcienną. Poniżej wymieniono kilka przykładów funkcji wielomianowych:

• y = x²
• y = 2x + 3
• y = 3x³

Funkcję wielomianową można dalej podzielić na następujące typy:

Funkcja liniowa : Funkcja liniowa to taka, w której maksymalna moc zmiennej wynosi 1. Ogólna postać Funkcja liniowa Jest y = mx + do

Funkcja kwadratowa : Funkcja kwadratowa to taka, w której maksymalna moc zmiennej wynosi 2. Ogólna postać funkcja kwadratowa Jest, topór ² + bx + do = 0

Funkcja sześcienna : Funkcja sześcienna to takie, w których maksymalna moc zmiennej wynosi 3. Ogólna postać funkcji sześciennej jest podana jako topór ³ + bx ² + cx + d = 0

Funkcja odwrotna

Funkcja odwrotna jest funkcją zawierającą odwrotność innej funkcji. Powiedzmy, że mamy funkcję y = f(x), wówczas jej funkcją odwrotną będzie x = f^-1(y). W y = f(x) dziedziną jest x, a zakresem jest y, natomiast w przypadku x = f^-1(y), dziedzina to y, a zakres to x. Można zatem powiedzieć, że dziedziną funkcji pierwotnej jest zakres jej funkcji odwrotnej, a zakres funkcji pierwotnej jest dziedziną funkcji pierwotnej. Oto kilka przykładów funkcji odwrotnych:

• y = tak^-1(X)
• y = x^-1

Funkcja obszaru

Funkcja powierzchni zazwyczaj odnosi się do funkcji matematycznej, która oblicza powierzchnię kształtu geometrycznego lub obszaru. Funkcja obszaru przyjmuje jeden lub więcej parametrów jako dane wejściowe i zwraca obszar odpowiedniego kształtu. Poniżej omówiono niektóre funkcje obszaru:

Pole funkcji okręgu : Powierzchnia koła (A) jest funkcją jego promienia (r) taką, że

A = πr ²

Pole funkcji trójkąta : Pole Trójkąta (A) jest funkcją jego podstawy (b) i wysokości (h) taką, że:

A = (bh)/2

Funkcja wykładnicza

Funkcja wykładnicza jest tym, który jest reprezentowany jako f(x) = e^X. Jest często używany do pokazania szybkiego wzrostu lub rozkładu.

Funkcja logarytmiczna

Funkcja logarytmiczna jest funkcją matematyczną reprezentującą odwrotną operację potęgowania. Jest reprezentowany jako f(x) = log x.

Funkcja sufitu

Funkcja sufitu , oznaczony jako ⌈x⌉, zaokrągla liczbę rzeczywistą x w górę do najbliższej liczby całkowitej większej lub równej x. Innymi słowy, znajduje najmniejszą wartość całkowitą, która jest większa lub równa x.

Funkcja podłogi

Funkcja podłogi, oznaczona jako ⌊x⌋, zaokrągla liczbę rzeczywistą x w dół do najbliższej liczby całkowitej mniejszej lub równej x. Innymi słowy, znajduje największą wartość całkowitą, która jest mniejsza lub równa x.

Funkcja modułu

Funkcja modułu , znana również jako funkcja wartości bezwzględnej, zwraca wielkość lub rozmiar liczby rzeczywistej bez względu na jej znak. Funkcja modułu jest oznaczana jako ∣x∣, gdzie x jest wartością wejściową.

jframe

Funkcja Signum

Funkcja znaku , znana również jako funkcja znaku lub funkcja znaku, to funkcja matematyczna zwracająca znak liczby rzeczywistej. Wskazuje, czy liczba jest dodatnia, ujemna czy zerowa.

Funkcje trygonometryczne

Funkcje trygonometryczne to funkcje matematyczne, które wiążą kąty trójkąta prostokątnego z długościami jego boków. Sześć podstawowych funkcji trygonometrycznych to sinus (sin), cosinus (cos), tangens (tan), cosecans (cosec), secans (s) i cotangens (cot).

Funkcje złożone

Wszelkie funkcje, w których zmienne wejściowe są funkcjami zespolonymi, nazywane są funkcjami zespolonymi. Liczba zespolona to liczba, którą można przedstawić na płaszczyźnie zespolonej. W Liczba zespolona mamy liczbę rzeczywistą i liczbę urojoną. Liczbę zespoloną (z) reprezentuje się jako z= x + iy, a funkcję zespoloną przedstawia się jako f(z) = P(x, y) + iQ(x, y)

Zastosowania funkcji

Kiedy mówimy, że zmienna wielkość y jest funkcją zmiennej wielkości x, wskazujemy, że y zależy od x i że wartość y jest określona przez wartość x. Zależność tę można wyrazić następująco: f = y (x).

• Promień okręgu można wykorzystać do obliczenia pola koła. Promień r wpływa na obszar A. Deklarujemy, że A jest funkcją r w matematycznym języku funkcji. Możemy zapisać A = f(r) =π×r²
• Objętość kuli V jest funkcją jej promienia. V = f(r) = 4/3×r³oznacza zależność V od r.
• Siła jest funkcją przyspieszenia ciała o ustalonej masie m. F = g(a) = m×a.

Ludzie czytali także:

• Relacja i funkcja
  
• Dziedzina i zakres funkcji trygonometrycznych
• Zakres funkcji
• Funkcja hiperboliczna

Przykłady dotyczące funkcji

Przykład 1: Dla dwóch funkcji f i g są zdefiniowane jako f(x) = x ² i g(x) = ln(2x). Znajdź funkcję złożoną (gof )( x )

Rozwiązanie:

Dany:

• f(x) = x²
• g(x) = ln(2x)

(gof)( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Zatem (gof)(x) = 2 ln(√2x)

Przykład 2: Znajdź wynik funkcji g(t)= 6t ² + 5 o godz

• (i) t = 0
• (ii) t = 2

Rozwiązanie:

Podana funkcja,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Przykład 3: Długość prostokąta jest pięciokrotnością jego szerokości. Pole prostokąta jest funkcją jego długości.

Rozwiązanie:

Niech długość prostokąta wynosi l, a szerokość prostokąta wynosi b

Teraz,

• b = l/5

Pole prostokąta(A) = l × l/5 = l²/5

Zatem pole prostokąta jako funkcja jego długości wynosi:

A(l) = l ² /5

Ćwicz problemy dotyczące tego, czym jest funkcja

1. Biorąc pod uwagę funkcję f(x)=3x+5

• Znajdź f(2)
• Znajdź f(−1)
• Określ dziedzinę i zakres funkcji.

2. Biorąc pod uwagę funkcję g(x)=x ² – 4x + 3

• Znajdź pierwiastki funkcji.
• Znajdź g(3) i g(0).
• Wyznacz wierzchołek funkcji.

3. Dane są dwie funkcje f(x)=x + 2 i h(x)=2x – 3

• Znajdź funkcję złożoną (f ∘ h) (x)
• Oszacuj (f ∘ h)(2)

Podsumowanie – Co to jest funkcja

Funkcja w matematyce to specjalna relacja między wartościami wejściowymi (dziedzina) i wartościami wyjściowymi (zakres), gdzie każde wejście jest powiązane z unikalnym wyjściem. Funkcje reprezentowane jako y = f(x) mają specyficzne cechy i można je wizualizować za pomocą uporządkowanych par, tabel lub wykresów. Są niezbędne w różnych problemach matematycznych i występują w różnych typach, w tym injektywnym (jeden do jednego), surjektywnym (na) i bijektywnym (oba). Funkcje można testować za pomocą testu linii pionowej i dzieli się je dalej na funkcje wielomianowe, odwrotne, wykładnicze, logarytmiczne i trygonometryczne. Zrozumienie funkcji polega na poznaniu ich dziedziny, zakresu i reguł je definiujących. Przykładami są proste funkcje liniowe, takie jak y = 2x + 1 i złożone kompozycje funkcji. Funkcje odgrywają kluczową rolę w algebrze, geometrii i rachunku różniczkowym, pomagając w reprezentacji i analizie zależności matematycznych i zjawisk w świecie rzeczywistym.

Często zadawane pytania dotyczące tego, czym jest funkcja

Jaka jest definicja funkcji?

Relacja f zdefiniowana w zbiorze A do innego zbioru B nazywana jest funkcją matematyczną, jeśli każda wartość A ma unikalną wartość w zbiorze B.

Jak napisać funkcję matematyczną?

Funkcja f w matematyce jest reprezentowana jako f: A → B i jest zdefiniowana jako: f(x) = x + 2. Tutaj dla każdej unikalnej wartości x mamy unikalną wartość y.

Jak przekształcić funkcję?

Możemy łatwo przekształcić funkcję w inną funkcję, po prostu wykonując na niej podstawowe operacje algebraiczne. Różne transformacje funkcji to odbicie, translacja, rotacja itp.

Co to jest funkcja wymierna?

Funkcja ułamkowa, w której licznik i mianownik są funkcjami wielomianowymi, nazywana jest funkcją wymierną. Niektóre przykłady funkcji wymiernej to:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), itp.

Co to jest funkcja liniowa?

Funkcja algebraiczna, w której każdy wyraz funkcji jest stały lub ma potęgę jedności, nazywa się funkcją liniową. Niektóre przykłady funkcji liniowej to:

• f(x) = 2x + 3
• g(x) = x – 5 itd.

Co to jest dziedzina i kodomena funkcji?

Jeśli zdefiniujemy tę funkcję jako, y = f(x). Wtedy dziedziną x są wszystkie wartości x, dla których y daje unikalną wartość. A współdziedzina y jest zbiorem wszystkich wartości y dla każdej wartości x.

Jak zidentyfikować funkcję w matematyce?

Jeśli jakakolwiek wartość wejściowa (x) dziedziny w relacji ma więcej niż jeden obraz (y), to relacja ta nigdy nie może być funkcją. Jeśli więc wartość x powtarza się w uporządkowanej parze, to nigdy nie jest to funkcja.