logo

TechCodeview

Linia symetrii

Linia symetrii: Linia symetrii, zwana także osią symetrii lub linią lustrzaną, to linia dzieląca kształt lub obiekt na dwie identyczne i symetryczne połowy. Każda połówka odzwierciedla drugą, dzięki czemu wyglądają jak wzajemne odbicia w poprzek linii, co wskazuje, że obie części kształtu będą idealnie dopasowane. Kształt nie zmieniłby się, gdyby wzdłuż tej linii ustawiono lustro.

W tym artykule omówimy koncepcję oś symetrii wraz z jej definicją i właściwościami. Będziemy także badać linie symetrii w alfabetach i linie symetrii w kształtach takich jak trójkąt, romb, równoległobok, pięciokąt itp.



Spis treści

Co to jest linia symetrii?

Linia symetrii to wyimaginowana linia, która dzieli kształt lub obiekt na symetryczne połowy. Krótko mówiąc, jedna połowa jest odbiciem drugiej połowy.

W Taj Mahal obserwujemy, że połowa po jednej stronie Taj Mahal jest taka sama, jak połowa po drugiej stronie, ponieważ każda strona jest doskonałym odbiciem lub lustrzanym odbiciem drugiej strony.



Jeśli przetniesz obiekt wzdłuż jego osi, powstanie lustrzane odbicie obu stron obiektu. Oś ta nazywana jest osią symetrii. Na przykład, jeśli przetniemy rozgwiazdę i ośmiornicę wzdłuż ich osi symetrii, otrzymamy podobne kształty.

Znaczenie linii symetrii

Oś symetrii to linia dzieląca obiekt na dwie równe części. Te dwie części są swoim lustrzanym odbiciem. Linia symetrii to wyimaginowana linia przechodząca przez środek obiektu.

Właściwości linii symetrii

Istnieje kilka właściwości pozwalających skutecznie zrozumieć koncepcję linii symetrii:



  • Jeśli ciało nie zawiera żadnej osi symetrii, wówczas oznacza to, że ciało jest asymetryczne.
  • Kształt lub bryła może mieć nieskończone linie symetrii. Na przykład w kręgach.
  • Obiekt może mieć jedną oś symetrii. Na przykład skrzydła motyla mają tylko jedną oś symetrii wzdłuż osi pionowej.
  • Niektóre obiekty mogą mieć dwie osie symetrii.

Sprawdzać: Symetria

Typy linii symetrii

Ogólnie rzecz biorąc, w różnych figurach geometrycznych można zaobserwować trzy rodzaje linii symetrii i są to:

  • Pozioma oś symetrii
  • Pionowa oś symetrii
  • Ukośna oś symetrii

Pozioma linia symetrii

Pozioma linia symetrii to śpiąca linia prosta, która dzieli kształt geometryczny na dwie równe połowy w sposób poziomy. W obiekcie przechodzi od lewej do prawej lub od prawej do lewej.

Pionowa linia symetrii

Pionowa linia symetrii to stojąca linia prosta, która dzieli kształt geometryczny na dwie równe połowy w sposób pionowy. W obiekcie przechodzi z góry na dół i odwrotnie.

Ukośna linia symetrii

Ukośna linia symetrii to ukośna linia dzieląca kształt geometryczny na dwie równe połowy na boki.

Linia symetrii dla różnych kształtów

W geometrii mamy kształty z jedną lub wieloma osiami symetrii zgodnie z ich strukturą, takie jak kwadrat, prostokąt, trójkąt, romb i równoległobok. Linie te mogą być poziome, pionowe lub ukośne. W kształtach dwuwymiarowych poznamy osie symetrii kolejnych kształtów

  • Oś symetrii w trójkącie
  • Linia symetrii w czworokącie
  • Linia symetrii w innych wielokątach
  • Linia symetrii w innych kształtach

Oś symetrii w trójkącie

Trójkąt to wielokąt ograniczony segmentami składającymi się z trzech linii. W zależności od długości boków istnieją trzy rodzaje trójkątów, a mianowicie Trójkąt równoboczny, Trójkąt równoramienny i Trójkąt równoramienny Trójkąt Skaleniczny.

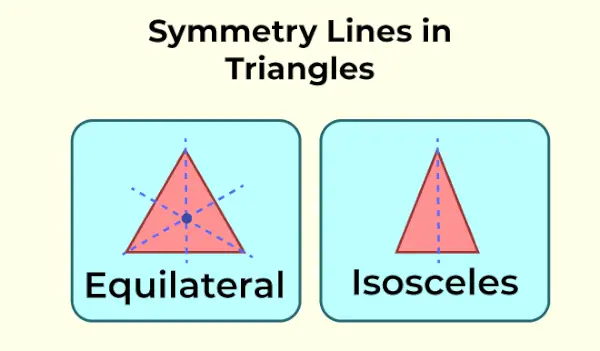
Oś symetrii w trójkątach

Oś symetrii w trójkącie równobocznym (symetria trzech linii)

Trójkąt równoboczny to trójkąt, w którym wszystkie boki są równe. Zatem trójkąt równoboczny ma trzy osie symetrii. Linie symetrii przechodzą od wierzchołka i środka przeciwnej strony.

Linia symetrii w trójkącie równoramiennym (symetria jednej linii)

Trójkąt równoramienny to trójkąt, w którym tylko dwa boki są równe. Zatem trójkąt równoramienny ma tylko jedną oś symetrii.

podciąg w Javie

Linia symetrii w trójkącie skalenowym (bez linii symetrii)

A trójkąt skalenowy jest trójkątem, w którym żadne boki nie są równe. Zatem Trójkąt Skalenowski nie ma osi symetrii.

Linia symetrii w czworokącie

Czworokąt to wielokąt, który ma cztery boki. Różne typy czworokątów to trapez, równoległobok, romb, kwadrat, prostokąt i latawiec. Dowiedzmy się o liniach symetrii w różnych czworokątach.

Oś symetrii w czworokątach

Linia symetrii w trapezie (bez linii symetrii)

A trapez jest czworokątem, w którym para przeciwnych boków jest równoległa. Trapez nie ma linii symetrii.

Linia symetrii w równoległoboku (bez linii symetrii)

Równoległobok to czworokąt, w którym przeciwne strony są równoległe i równe. Parllelogramn nie ma osi symetrii.

Linia symetrii w latawcu (symetria jednej linii)

Latawiec zawiera jedną oś symetrii. Ta linia symetrii w latawcu ma charakter pionowy.

Oś symetrii w prostokącie (symetria dwóch linii)

Prostokąt ma dwie osie symetrii: jedną pionową i jedną poziomą oś symetrii. Linie te przechodzą przez środki przeciwnych stron. Złożona po przekątnej nadaje asymetryczny kształt.

Linia symetrii w rombie (symetria dwóch linii)

A romb ma dwie osie symetrii. Te dwie osie symetrii rombu są jego przekątnymi.

Oś symetrii w kwadracie (symetria czterech linii)

Kwadrat ma cztery osie symetrii: jedną pionową, jedną poziomą i dwie ukośne osie symetrii. Cztery osie symetrii są utworzone przez linie przechodzące przez środki przeciwległych boków.

Linia symetrii w wyższych wielokątach

Wiemy, że wielokąt to zamknięta figura ograniczona trzema lub większą liczbą odcinków. Powyżej dowiedzieliśmy się o liniach symetrii trójkątów i czworokątów. Dowiedzmy się o liniach symetrii w wyższych wielokątach, takich jak pięciokąt, sześciokąt itp.

Linia symetrii w wyższych wielokątach

Linia symetrii w Pentagonie (symetria pięciu linii)

Regularny pięciokąt ma pięć osi symetrii: jedną poziomą, jedną pionową i trzy ukośne.

Linia symetrii w sześciokącie (symetria sześciu linii)

Regularny sześciokąt zawiera sześć osi symetrii: jedną poziomą, jedną pionową i cztery ukośne.

Linia symetrii w siedmiokącie (symetria siedmiu linii)

Zwykły siedmiokąt ma 7 równych boków. Zatem w Heptagonie jest 7 osi symetrii.

Linia symetrii w ośmiokącie (symetria ośmiu linii)

Ośmiokąt zawiera osiem osi symetrii. Z tych 8 linii symetrii cztery to poziome linie symetrii, a cztery to pionowe linie symetrii

Linia symetrii w innych kształtach

W tym nagłówku poznajemy linie symetrii innych kształtów, takich jak okrąg i gwiazda. Ponieważ okrąg może składać się wzdłuż linii średnicy, stąd wszystkie osie symetrii koła będą przebiegać wzdłuż jego średnicy. W przypadku gwiazdy osie symetrii przebiegają wzdłuż linii łączących przeciwległe wierzchołki.

Linia symetrii w okręgu i gwieździe

Linia symetrii w okręgu (nieskończone linie symetrii)

Okrąg ma nieskończoną liczbę linii symetrii, ponieważ jest symetryczny wzdłuż swojej nieskończonej osi, a przez jego środek może przechodzić nieskończona liczba linii.

Linia symetrii gwiazdy (symetria pięciu linii)

W Gwieździe linie Symetrii przechodzą przez przeciwne wierzchołki. Zatem w gwieździe jest w sumie pięć osi symetrii.

Linia symetrii w alfabecie

Oprócz kształtów geometrycznych alfabety angielskie mają również osie symetrii. Poniżej wymienione tematy wyjaśniają osie symetrii w alfabecie angielskim.

Linia symetrii w alfabecie

dynamiczna tablica w Javie

Pionowa linia symetrii w alfabecie angielskim

Alfabety angielskie ze względu na pionową oś symetrii to A, H, I, M, O, T, U, V, W, X, Y.

Pozioma linia symetrii w alfabecie angielskim

Alfabety angielskie ze względu na poziomą oś symetrii to B, C, D, E, H, I, K, O, X.

Dwie linie symetrii (pozioma i pionowa) w alfabecie angielskim

Litery posiadające poziome i pionowe osie symetrii to H, I, O, X.

Zerowa linia symetrii w alfabecie angielskim

Alfabety takie jak F, G, L, P, Q, R, S, Z nie mają osi symetrii.

Oś symetrii równań

Istnieje kilka sposobów znalezienia osi symetrii. W układzie współrzędnych wykres może mieć symetrię względem osi x, osi y, początku układu współrzędnych lub względem dowolnej linii.

Na przykład parabola ma symetrię linii w geometrii współrzędnych i równanie symetrii linii dla paraboli z równaniem kwadratowym y = ax2+ bx + c ma postać x = n, gdzie n jest liczbą rzeczywistą, a a i b są współczynnikami x2i x odpowiednio i c jest stałą. x = -b/(2a) daje nam naszą oś symetrii.

Oznacza to, że osią symetrii jest linia pionowa przechodząca przez x = -b/(2a). Linia ta podzieli parabolę na dwie równe połowy.

Na przykład, jeśli otrzymamy równanie paraboli w standardowej postaci, takiej jak y = x2+ 6x + 3, wiemy, że a=1, b=6 i c=3. Tutaj możemy umieścić wartość aib we wzorze x=−b/2a, aby otrzymać oś symetrii. Formuła przyjmuje postać x =−(6)/2(1), co daje x = −3. Oznacza to, że osią symetrii jest linia pionowa przechodząca przez x=−3.

Ludzie czytali także:

Przykłady linii symetrii

Przykład 1. Znajdź oś symetrii paraboli y = -2x 2 − 4x + 8.

Rozwiązanie:

Dane równanie: y = -2x2− 4x + 8

Porównaj podane równanie ze standardową formą ax2+ bx + c.

⇒ a = -2, b = -4, do = 8

Skorzystaj ze wzoru na oś symetrii = −b/2a

= −(−4)/2(-2) ⇒ x = 1

Równanie prostej osi symetrii to x=1.

Przykład 2. Znajdź oś symetrii paraboli y = 4x 2 .

Rozwiązanie:

Dane równanie: y = 4x2

Porównaj podane równanie ze standardową formą ax2+ bx + c.

⇒ a = 4, b = 0, do = 0

Skorzystaj ze wzoru na oś symetrii = −b/2a

= -0/2(4) ⇒ x = 0

Przykład 3. Jak zlokalizować linie symetrii kształtu?

Rozwiązanie:

Najpierw złożymy kształt wzdłuż linii w taki sposób, aby jedna połowa była dokładnie podobna do drugiej. Linia ta nazywana jest linią symetrii.

Przykład 4. Ile linii symetrii można narysować na pięciokącie foremnym?

Rozwiązanie:

Oś symetrii dzieli figurę na dwa identyczne odbicia lustrzane. W pięciokącie foremnym można narysować łącznie 5 linii symetrii: jedną poziomą, jedną pionową i trzy ukośne.

Przykład 5. Jaki jest standardowy wzór na oś symetrii paraboli?

Rozwiązanie:

Standardowy wzór na oś symetrii równania (y=ax2+ bx + c) wynosi x = −b/2a

Ćwicz pytania dotyczące linii symetrii

Pytanie 1. Narysuj wszystkie osie symetrii trójkąta równobocznego.

Pytanie 2. Narysuj wszystkie osie symetrii pięciokąta foremnego.

Pytanie 3. Ile osi symetrii można narysować w okręgu?

Pytanie 4. Ile osi symetrii można narysować w trójkącie równoramiennym i trójkącie pochyłym?

Pytanie 5. Ile alfabetów ma dokładnie dwie osie symetrii?

Pytanie 6. Ile alfabetów ma dokładnie jedną oś symetrii?

Pytanie 7. Zapisz oś symetrii równania kwadratowego y = x2+18x+8.

Linia symetrii – często zadawane pytania

Czym jest symetria w matematyce?

Symetria w matematyce to stan posiadania dwóch równych połówek, które dokładnie pasują do siebie pod względem wielkości i kształtu, gdy dzielą się wzdłuż wyimaginowanej linii.

Ile osi symetrii ma prostokąt?

Prostokąt ma dwie osie symetrii: jedną pionową i jedną poziomą oś symetrii.

Ile osi symetrii ma kwadrat?

Kwadrat ma cztery osie symetrii: jedną pionową, jedną poziomą i dwie ukośne osie symetrii.

Ile osi symetrii ma romb?

Romb ma 2 osie symetrii: dwie przekątne.

Ile osi symetrii ma równoległobok?

Zerowa linia symetrii.

Ile linii symetrii ma latawiec?

Tylko jedna oś symetrii: pionowa.

Ile linii symetrii ma gwiazda?

Sześciogwiazdkowa gwiazda ma sześć osi symetrii

Co to jest oś symetrii?

Oś symetrii definiuje się jako wyimaginowaną linię, wzdłuż której figurę lub kształt można złożyć lub podzielić na dwie symetryczne połowy.

Ile osi symetrii można narysować w półkolu?

W półkolu można narysować tylko jedną symetryczną linię.

Ile linii symetrii może przejść przez angielski alfabet H?

Przez H mogą przechodzić dwie linie symetrii: jedna pozioma i jedna pionowa.

Który trójkąt nie ma osi symetrii?

Trójkąt skalenowy nie zawiera żadnej osi symetrii. Jest to trójkąt asymetryczny.

Które kształty nie mają linii symetrii?

Trójkąt skalenowy, trapez, równoległobok itp. nie mają osi symetrii.

co to jest ur