Wielokąt w matematyce to dwuwymiarowy kształt złożony z prostych linii tworzących zamknięty wielokątny łańcuch. Słowo wielokąt pochodzi od słów poli i gon, które oznaczają wiele i boki.
Wielokąty mogą być proste lub samoprzecinające się. Prosty wielokąt nie przecina się sam ze sobą, z wyjątkiem wspólnych punktów końcowych kolejnych segmentów. Łańcuch wielokątny, który przecina się sam ze sobą, tworzy samoprzecinający się wielokąt. Wielokąty można również podzielić na wklęsłe i wypukłe.
W tym artykule szczegółowo wspomnieliśmy o wielokątach, ich typach, formułach i przykładach.
| Ważne fakty na temat wielokątów | |
|---|---|
| Suma kątów wewnętrznych wielokąta | (n–2) × 180° |
| Liczba przekątnych w wielokącie | n(n–3)/2 |
| Kąt wewnętrzny wielokąta foremnego | {(n–2) × 180°}/n |
| Kąt zewnętrzny wielokąta foremnego | 360°/n |
Spis treści
- Co to są wielokąty?
- Wykres wielokątny oparty na liczbie boków
- Właściwości wielokątów
- Kształty wielokątów
- Rodzaje wielokątów
- Formuły wielokątów
- Kąty w wielokątach
- Często zadawane pytania
Co to są wielokąty?
Termin „wielokąt” pochodzi od greckiego słowa polugonos, gdzie „poly” oznacza „wiele”, a „gon” oznacza „kąt”. Ogólnie rzecz biorąc, wielokąt to zamknięta figura utworzona przez linie proste, z utworzonymi przez nie kątami wewnętrznymi linie. Aby utworzyć zamkniętą bryłę, potrzebne są minimum trzyliniowe segmenty. Jest powszechnie znany jako trójkąt lub 3-kąt. Ogólnym określeniem wielokąta n-stronnego jest n-kąt.
Definicja wielokąta
Wielokąty to płaskie, dwuwymiarowe figury złożone z prostych boków, które tworzą całkowicie zamknięty kształt. W geometrii wielokąt jest płaską figurą złożoną z odcinków połączonych w zamknięty łańcuch wielokątny. Składają się z prostych boków, a nie krzywych, i mogą mieć dowolną liczbę boków. Niektóre wielokąty różnego rodzaju to: otwarte, tylko graniczne, zamknięte i samoprzecinające się.
W geometrii wielokąt definiuje się jako zamknięty, dwuwymiarowy kształt, który leży płasko na płaszczyźnie i jest otoczony prostymi bokami.
Wielokąt nie ma zakrzywionych boków, a jego krawędzie są prostymi segmentami wyznaczającymi jego granicę. Punkty styku tych krawędzi nazywane są wierzchołkami lub narożnikami.
Przykłady wielokątów
Pod względem matematycznym przykładami wielokątów są trójkąty, sześciokąty, pięciokąty i czworoboki. Prawdziwymi przykładami Polygon są prostokątny ekran laptopa, telewizora, telefonu komórkowego; prostokątne boisko do piłki nożnej lub plac zabaw, Trójkąt Bermudzki i egipskie piramidy o trójkątnym kształcie.

Części wielokąta
Wielokąt składa się z trzech podstawowych elementów:
- Boki wielokąta: Boki wielokątów są granicami wielokątów definiujących zamknięty obszar.
- Wierzchołki: Punkt, w którym spotykają się dwie strony, nazywany jest wierzchołkiem.
- Kąty: Wielokąt zawiera zarówno kąty wewnętrzne, jak i zewnętrzne. Kąt wewnętrzny jest utworzony w zamkniętym obszarze wielokąta przez przecięcie jego boków.
Wykres wielokątny oparty na liczbie boków
Nomenklatura wielokątów zdefiniowana na podstawie liczby posiadanych boków. Oznacza się go jako n-gon, gdzie „n” oznacza liczbę boków. Wielokąty są zazwyczaj identyfikowane przez liczbę ich krawędzi. Na przykład wielokąt z pięcioma bokami nazywany jest pięciokątem, a wielokąt z dziesięcioma bokami określany jest jako 10-kątny.
| Wykres wielokątny | ||||
|---|---|---|---|---|
| Nazwy kształtów wielokątów | Liczba boków | Liczba wierzchołków | Liczba przekątnych | Miara kąta wewnętrznego dla regularnego kształtu |
| Trójkąt | Wielokąty mające 3 boki | 3 obiekt w Javie | 0 | 60° |
| Czworoboczny | Wielokąty mające 4 boki | 4 | 2 | 90° |
| Pięciokąt | Wielokąty mające 5 boków | 5 | 5 | 108° |
| Sześciokąt | Wielokąty mające 6 boków | 6 | 9 | 120° |
| Siedmiokąt | Wielokąty mające 7 boków | 7 | 14 | 128,571° |
| Ośmiokąt | Wielokąty mające 8 boków | 8 | 20 | 135° |
| Nonagon | Wielokąty mające 9 boków tabela w reakcji | 9 | 27 | 140° |
| Dekagon | Wielokąty mające 10 boków | 10 | 35 | 144° |
| Hendecagon | Wielokąty mające 11 boków | jedenaście | 44 | 147,273° |
| Dwunastokąt | Wielokąty mające 12 boków | 12 | 54 | 150° |
Właściwości wielokątów
Właściwości wielokątów łatwo je identyfikują. Następujące właściwości przyczyniają się do łatwego poznania wielokątów:
- Wielokąt to zamknięty kształt, pozbawiony otwartych końców. Początek i punkt końcowy powinny być takie same.
- Przyjmuje formę planarną, składającą się z odcinków linii lub linii prostych, które wspólnie kształtują figurę.
- Jako byt dwuwymiarowy wielokąt istnieje tylko w wymiarach długości i szerokości, bez głębokości i wysokości.
- Posiada trzy lub więcej boków, aby utworzyć wielokąt.
- Kąty w wielokącie mogą się różnić. Pokazuje odrębną konfigurację.
- Długość boków wielokąta może się różnić; może, ale nie musi, być równy w całym wielokącie.
Kształty wielokątów
Wielokąt to płaski, dwuwymiarowy kształt charakteryzujący się prostymi bokami połączonymi w zamkniętą figurę. Przykłady kształtów wielokątów obejmują:
- Trójkąt
- Czworoboczny
- Pięciokąt
- Sześciokąt
- Siedmiokąt
- Ośmiokąt
- Nonagon
- Dekagon
Trójkąt
- Ma 3 boki i 3 wierzchołki.
- Nie ma przekątnych.
- Suma wnętrza wynosi 180°.
Czworoboczny
- Ma 4 boki i 4 wierzchołki.
- Ma 2 przekątne.
- Suma kątów wewnętrznych wynosi 360°.
Pięciokąt
- Ma 5 boków i 5 wierzchołków.
- Ma 5 przekątnych.
- Suma kątów wewnętrznych wynosi 540°.
Sześciokąt
- Ma 6 boków i 6 wierzchołków.
- Ma 9 przekątnych.
- Suma kątów wewnętrznych wynosi 720°.
Siedmiokąt
- Ma 7 boków i 7 wierzchołków.
- Ma 14 przekątnych.
- Suma kątów wewnętrznych wynosi 900°.
Ośmiokąt
- Ma 8 boków i 8 wierzchołków.
- Ma 20 przekątnych.
- Suma kątów wewnętrznych wynosi 1080°.
Nonagon
- Ma 9 boków i 9 wierzchołków.
- Ma 27 przekątnych.
- Suma kątów wewnętrznych wynosi 1260°.
Dekagon
- Ma 10 boków i 10 wierzchołków.
- Ma 35 przekątnych.
- Suma kątów wewnętrznych wynosi 1440°.
Rodzaje wielokątów
W zależności od boków i kątów wielokąty można podzielić na różne typy na różnych podstawach, takie jak:
- Na podstawie stron
- Na podstawie kątów
- Na podstawie granicy
Wielokąty na podstawie boków
Wielokąty można podzielić na dwa podstawowe typy na podstawie cech ich boków:
- Regularny wielokąt
- Nieregularny wielokąt
Regularny wielokąt
Wielokąt foremny wyróżnia się tym, że wszystkie boki mają jednakową długość i wszystkie kąty wewnętrzne mają równe wymiary. Może być zarówno równoboczny, jak i równokątny. Przykłady regularnych wielokątów obejmują trójkąt, czworokąt, pięciokąt i sześciokąt.

Regularny wielokąt
Nieregularny wielokąt
Wielokąt nieregularny ma boki o różnej długości i kąty o różnej mierze. Każdy wielokąt, który nie spełnia kryteriów wielokąta foremnego, jest klasyfikowany jako nieregularny. Typowymi przykładami nieregularnych wielokątów są trójkąt skalenowy, czworoboki, takie jak prostokąt, trapez lub latawiec, a także nieregularne struktury pięciokątne i sześciokątne.
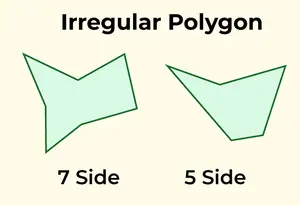
Nieregularny wielokąt
Wielokąty na podstawie kątów
Wielokąty można klasyfikować na podstawie charakteru ich kątów na dwie główne kategorie:
- Wielokąt wypukły
- Wklęsły wielokąt
Wielokąt wypukły
Wielokąt wypukły nie ma kąta wewnętrznego o mierze większej niż 180°. Wielokąty wypukłe mogą mieć trzy lub więcej boków. W wielokątach wypukłych wszystkie przekątne leżą wewnątrz zamkniętej figury. Typowymi przykładami wielokątów wypukłych są trójkąty, wszystkie wypukłe czworoboki, a także regularne pięciokąty i sześciokąty
Wklęsły wielokąt
Wklęsły wielokąt ma co najmniej jeden kąt wewnętrzny, który jest kątem odruchowym i jest skierowany do wewnątrz. Wklęsłe wielokąty mają co najmniej cztery boki. Ten typ wielokąta ma co najmniej jeden kąt wewnętrzny o mierze większej niż 180°. We wklęsłych wielokątach niektóre przekątne wystają poza zamkniętą figurę. Przykłady wklęsłych wielokątów obejmują strzałkę lub grot strzały w czworokątach, a także niektóre nieregularne pięciokąty i sześciokąty.
Różnica między wielokątami wklęsłymi i wypukłymi
Zobaczmy różnicę między wielokątem wypukłym i wklęsłym w poniższej tabeli:

| Wielokąt wypukły | Wklęsły wielokąt |
|---|---|
| Cały obwód wypukłego kształtu rozciąga się na zewnątrz bez żadnych wgłębień do wewnątrz. | Kształt wklęsły ma co najmniej jedną część skierowaną do wewnątrz, co wskazuje na obecność wgniecenia. |
| W wielokącie wypukłym wszystkie kąty wewnętrzne mają mniej niż 180°. | W wielokącie wklęsłym istnieje co najmniej jeden kąt wewnętrzny przekraczający 180°. |
| Dowolna linia łącząca dwa wierzchołki kształtu wypukłego leży całkowicie w granicach kształtu. co to jest f5 na klawiaturze | Linia łącząca dowolne dwa wierzchołki wklęsłego kształtu może, ale nie musi, przecinać wnętrze kształtu. |
Wielokąty na podstawie granic
Wielokąty można podzielić na dwa podstawowe typy w oparciu o charakter ich granic:
- Prosty wielokąt
- Złożony wielokąt
Prosty wielokąt
Prosty wielokąt charakteryzuje się pojedynczą, nieprzecinającą się granicą. Innymi słowy, nie przecina się i składa się z jednej granicy.
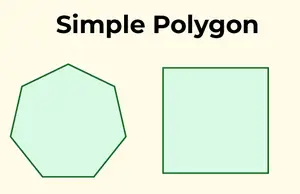
Proste wielokąty
Złożony wielokąt
Z drugiej strony wielokąt złożony jest definiowany przez samo przecięcie. Składa się z więcej niż jednej granicy w swojej strukturze. W złożonych wielokątach granica przecina się, tworząc wiele odrębnych regionów w obrębie wielokąta.

Złożony wielokąt
Przeczytaj więcej na temat Rodzaje wielokątów.
Formuły wielokątów
Istnieje kilka wzorów związanych z wielokątami w geometrii. Do najczęściej używanych należą:
- Formuła obszaru
- Wzór obwodu
- Liczba przekątnych
Wszystkie wzory związane z różnymi wielokątami omówiono poniżej:
Powierzchnia wielokątów
Powierzchnia wielokąta reprezentuje całkowitą przestrzeń, jaką zajmuje na płaszczyźnie dwuwymiarowej, jest wyznaczana za pomocą specjalnych wzorów opartych na liczbie boków i klasyfikacji wielokąta. Formuły powierzchni są następujące:
| Powierzchnia wielokąta | Formuła |
|---|---|
| Pole Trójkąta | 1/2 × podstawa × wysokość |
| Pole równoległoboku | Podstawa × wysokość |
| Pole prostokąta | Długość × szerokość |
| Powierzchnia Kwadratu | (Strona)2 |
| 1/2 × przekątna1× przekątna2 | |
| Powierzchnia trapezu | 1/2 × wysokość × suma boków równoległych |
| (5/2) × długość boku × Apothem | |
| Powierzchnia sześciokąta | {(3√3)/2}strona2 |
| Obszar Heptagonu | 3,643 × bok2 |
Obwód wielokątów
Obwód dwuwymiarowego kształtu reprezentuje całkowitą długość jego zewnętrznej granicy. W przypadku wielokątów obwód oblicza się w następujący sposób:
| Obwód wielokąta | Formuła |
|---|---|
| Obwód trójkąta | Suma trzech stron |
| Obwód równoległoboku | 2(Suma sąsiednich boków) |
| Obwód prostokąta | 2 (długość + szerokość) |
| Obwód kwadratu | 4 × Bok |
| Obwód rombu | 4 × Bok |
| Obwód trapezu | Suma boków równoległych + suma boków nierównoległych |
| Obwód Pentagonu | 5 × Bok |
| Obwód sześciokąta | 6 × Bok np.gdzie |
| Obwód siedmioboku | 7 × Bok |
Przekątna wzoru wielokąta
Przekątna wielokąta to odcinek utworzony przez połączenie dwóch wierzchołków, które nie sąsiadują ze sobą.
Liczba przekątnych w wielokącie = n(n−3)/2,
Gdzie „n” oznacza liczbę boków wielokąta.
Przeczytaj więcej na temat Przekątna wzoru wielokąta .
Kąty w wielokątach
W geometrii kąty w wielokątach odnoszą się do kątów utworzonych przez boki wielokąta, zarówno wewnątrz, jak i na zewnątrz wielokąta. Zatem w wielokącie mogą występować oba kąty, tj.
- Kąty wewnętrzne
- Kąty zewnętrzne
Omówmy szczegółowo wzór na te kąty w następujący sposób:
Wzór kąta wewnętrznego wielokątów
Kąty wewnętrzne wielokąta to kąty utworzone pomiędzy sąsiednimi bokami i są równe w przypadku wielokąta foremnego. Liczba kątów wewnętrznych odpowiada liczbie boków wielokąta.
Sumę kątów wewnętrznych „S” w wielokącie o „n” bokach oblicza się jako:
S = (n – 2) × 180°
Gdzie „n” oznacza liczbę boków.
Wzór kąta zewnętrznego wielokątów
Każdy kąt zewnętrzny wielokąta foremnego jest tworzony przez przedłużenie jednego z jego boków (zgodnie z ruchem wskazówek zegara lub przeciwnie do ruchu wskazówek zegara) i zmierzenie kąta między tym przedłużeniem a sąsiednim bokiem. W wielokącie foremnym wszystkie kąty zewnętrzne są równe
Całkowita suma kątów zewnętrznych w dowolnym wielokącie jest ustalona na 360°
Dlatego,
Każdy kąt zewnętrzny jest określony przez 360°/n
Gdzie „n” to liczba boków.
Suma kątów wewnętrznych i odpowiadających im kątów zewnętrznych w dowolnym wierzchołku wielokąta wynosi zawsze 180 stopni, co wyraża dodatkową zależność:
Kąt wewnętrzny + Kąt zewnętrzny = 180°
Kąt zewnętrzny = 180° – Kąt wewnętrzny
Wniosek
- Wielokąt to zamknięta figura ograniczona trzema lub większą liczbą odcinków linii
- Suma kątów wewnętrznych: Sumę wszystkich kątów wewnętrznych w wielokącie n-stronnym można wyrazić wzorem (n–2)×180°.
- Liczba przekątnych: Dla wielokąta o n bokach liczbę przekątnych oblicza się ze wzoru n(n–3)/2.
- Trójkąty utworzone przez przekątne: Liczba trójkątów utworzonych przez połączenie przekątnych z jednego narożnika wielokąta wynosi n–2.
- Kąt wewnętrzny wielokąta foremnego: Miara każdego kąta wewnętrznego w wielokącie foremnym n-stronnym wynosi {(n–2) × 180°}/n.
- Kąt zewnętrzny wielokąta foremnego: Miara każdego kąta zewnętrznego w wielokącie foremnym n-stronnym wynosi 360°/n.
Przeczytaj także
- Kwadrat
- Równoległobok
- Prostokąt
Rozwiązane przykłady wielokątów w matematyce
Przykład 1: Rozważmy czworokąt z czterema bokami. Znajdź sumę wszystkich kątów wewnętrznych czworoboku.
Rozwiązanie:
Wzór na sumę kątów wewnętrznych w wielokącie foremnym n-stronnym = (n - 2) × 180°
Suma wszystkich kątów wewnętrznych czworokąta = (4 – 2) × 180°
Suma wszystkich kątów wewnętrznych czworokąta = 2 × 180°
Suma wszystkich kątów wewnętrznych czworokąta = 360°
Zatem suma wszystkich kątów wewnętrznych czworokąta wynosi 360°.
Przykład 2: Rozważmy wielokąt foremny o danym stosunku kątów zewnętrznych i wewnętrznych wynoszącym 7:3. Określ typ wielokąta.
Rozwiązanie:
Stosunek kąta zewnętrznego i wewnętrznego wynosi 7:3.
Załóż, że kąt zewnętrzny i wewnętrzny wielokąta wynosi 7x i 3x.
Suma kątów zewnętrznych i wewnętrznych dowolnego wielokąta wynosi 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Kąt zewnętrzny = 18°
Liczba boków = 360°/kąt zewnętrzny
= 360°/18°
logika zdań= 20
Dlatego dany wielokąt jest ikosagonem, ponieważ ma 20 boków.
Przykład 3: Każdy kąt zewnętrzny wielokąta ma miarę 90 stopni. Określ typ wielokąta?
Rozwiązanie:
Zgodnie ze wzorem każdy kąt zewnętrzny = 360°/n
Tutaj n=liczba boków.
90°= 360°/n
n = 360°/90°= 4
Zatem wielokąt, o którym mowa, jest czworokątem, ponieważ ma cztery boki.
Przykład 4: Boki mają długości 10 m, 10 m, 8 m, 8 m, 5 m, 5 m, 9 m, 9 m. Ile metrów liny będzie potrzebne do wykonania obwodu?
Rozwiązanie:
Aby znaleźć długość liny potrzebną na obwód, musimy zsumować długości wszystkich boków:
Obwód = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Obwód = 64 m.
Dlatego na obwód potrzebne będą łącznie 64 metry liny.
Ćwicz pytania dotyczące wielokątów w geometrii
Poniżej znajduje się kilka praktycznych pytań opartych na wzorze wielokątów:
Pytanie 1. Biorąc pod uwagę, że jeden kąt pięciokąta wynosi 140°, określ wielkość największego kąta, jeśli pozostałe kąty są w stosunku 1:2:3:4.
Pytanie 2. Znajdź liczbę boków wielokąta, jeśli suma kątów wewnętrznych wielokąta wynosi 160°.
Pytanie 3. Liczba boków w dwóch wielokątach foremnych jest stosunek 2:3, a stosunek ich kątów wewnętrznych wynosi 4:5. Znajdź odpowiednie liczby boków tych wielokątów.
Pytanie 4. Wyznacz całkowitą sumę kątów w siedmiokącie.
Pytanie 5. Oblicz sumę kątów zewnętrznych w pięciokącie.
Pytanie 6. Ile boków ma sześciokąt?
- 4
- 6
- 8
- 10
Pytanie 7. Który z poniższych nie jest wielokątem foremnym?
- Trójkąt
- Kwadrat
- Pięciokąt
- Równoległobok
Często zadawane pytania dotyczące wielokątów w matematyce
Co to jest wielokąt w matematyce?
W matematyce wielokąt odnosi się do zamkniętej dwuwymiarowej figury utworzonej przez połączenie trzech lub więcej linii prostych. Termin wielokąt pochodzi z języka greckiego, gdzie wielokąt oznacza wiele, a gon reprezentuje kąt.
Który wielokąt jest najmniejszy?
Najmniejszym utworzonym wielokątem jest trójkąt o trzech bokach.
Co to jest 20-gon?
20-kąt jest dwudziestobocznym wielokątem w geometrii.
Jaka jest całkowita suma kątów zewnętrznych wielokąta?
Suma kątów zewnętrznych wielokąta wynosi 360°.
Czy okrąg można sklasyfikować jako wielokąt?
Wielokąt to zamknięty kształt złożony z prostych segmentów. Okrąg jest figurą zamkniętą, ale składa się z krzywej. Zatem okrąg nie jest wielokątem.
Jaka jest suma kątów wewnętrznych wielokąta?
Sumę kątów wewnętrznych wielokąta wyraża się wzorem (n–2)×180°, gdzie n jest liczbą boków wielokąta.
